26 min to read

Player Similarity Models

Exploring player similarity analysis in football

Featured image

In my last post we explored the use of K-Means Clustering to identify the roles of the players within teams from a statistical perspective. I will take that concept further and now use the same concepts to to build a player similarity model using data from FBREF.

Introduction: Unveiling Similarities - K-Means Clustering and Euclidean Distance

The ever-growing realm of sports analytics thrives on uncovering hidden patterns and relationships within vast datasets. Player performance metrics, scouting reports, and player attributes – all these elements paint a complex picture of an athlete’s capabilities. But how can we effectively analyze this data to identify similar player profiles or categorize distinct playing styles? Enter the realm of unsupervised machine learning, where algorithms like K-means clustering come into play.

Imagine a vast collection of player data points, each representing a unique athlete. K-means steps in, analyzing these data points and strategically dividing them into distinct clusters, ensuring that players with similar attributes end up grouped together.

This process allows us to discover patterns and categorize players based on analogous characteristics.

We can then leverage these insights to identify potential player replacements, scout for specific skillsets.

In simpler terms, K-means acts like a sophisticated sorting mechanism, organizing data points based on their “closeness” in a multidimensional space.

This concept of “closeness” is quantified by a mathematical measure known as Euclidean distance. But before we delve deeper into K-means, let’s establish a solid foundation in Euclidean distance, the cornerstone for measuring similarity in K-means clustering.

Demystifying Euclidean Distance: A Measure of Closeness

Euclidean distance, named after the ancient Greek mathematician Euclid, is a fundamental concept in geometry that calculates the straight-line distance between two points in space. Imagine two players, Player A and Player B, represented by data points in a multidimensional space where each dimension corresponds to a specific attribute (e.g., shooting accuracy, passing success rate, etc.). Euclidean distance helps us quantify how “similar” these players are based on their combined attributes.

The mathematical formula for Euclidean distance between two points (represented by vectors x and y) in an n-dimensiona space is as follows:

d(x, y) = √((x₁ - y₁)² + (x₂ - y₂)² + … + (xₙ - yₙ)²)

Here, d(x, y) represents the Euclidean distance between points x and y, n denotes the number of dimensions (i.e., number of player attributes), and (xᵢ - yᵢ) represents the difference between the corresponding values of the i-th attribute for players A and B. This equation essentially calculates the square root of the sum of squared differences along each dimension.

For instance, if Player A has a higher shooting accuracy but a lower passing success rate compared to Player B, the Euclidean distance will reflect this difference, indicating that these players exhibit some level of dissimilarity. Conversely, a small Euclidean distance between two players suggests a high degree of similarity in their overall skillset.

Key Points about Euclidean Distance:

It measures the “straight-line” distance between two points in a multidimensional space. A smaller distance signifies greater similarity between data points. It is a foundational concept for K-means clustering, used to determine the “closeness” of data points to cluster centroids. With a firm grasp of Euclidean distance, we are now prepared to explore the inner workings of the K-means clustering algorithm and its application in building player similarity models.*

Finding Similar Players

I will leverage the K-Means model made in my last post as a basis for our Euclidean distance calculation. Further changes I have made include now using the all player data from European Top 5 Leagues,instead of just the EPL, to broaden the number of players available.


# Top 5 Europeans Leagues for advanced Analysis 

fbref_passing = 'https://fbref.com/en/comps/Big5/passing/players/Big-5-European-Leagues-Stats'
fbref_shooting = 'https://fbref.com/en/comps/Big5/shooting/players/Big-5-European-Leagues-Stats'
fbref_pass_type = 'https://fbref.com/en/comps/Big5/passing_types/players/Big-5-European-Leagues-Stats'
fbref_defence = 'https://fbref.com/en/comps/Big5/defense/players/Big-5-European-Leagues-Stats'
fbref_gca = 'https://fbref.com/en/comps/Big5/gca/players/Big-5-European-Leagues-Stats'
fbref_poss = 'https://fbref.com/en/comps/Big5/possession/players/Big-5-European-Leagues-Stats'
fbref_misc = 'https://fbref.com/en/comps/Big5/misc/players/Big-5-European-Leagues-Stats'


stats = create_full_stats_db(fbref_passing,fbref_shooting,fbref_pass_type,fbref_defence,fbref_gca,fbref_poss,fbref_misc)

Filtering and Preprocessing Key Statistics

We define a function that filters the dataset to include only players of a specific position and removes any rows with missing values. Additionally, the player statistics are adjusted to a per-90-minute basis to ensure fair comparisons among players with varying playtime.

def key_stats_db(df, position):
    non_numeric_cols = ['Player', 'Nation', 'Pos', 'Squad', 'Age', 'position_group']
    core_stats = ['90s','Total - Cmp%','KP', 'TB','Sw','PPA', 'PrgP','Tkl%','Blocks', 'Tkl+Int','Clr', 'Carries - PrgDist','SCA90','GCA90','CrsPA','xA', 'Rec','PrgR','xG', 'Sh','SoT']
    df.dropna(axis=0, how='any', inplace=True)
    key_stats_df = df[df['position_group'] == position]
    key_stats_df = key_stats_df[non_numeric_cols + core_stats]
    key_stats_df = key_stats_df[key_stats_df['90s'] > 5]
    key_stats_df = per_90fi(key_stats_df)
    return key_stats_df

key_stats_df = key_stats_db(stats, position)

Explanation:

  1. Defines a function key_stats_db to filter and preprocess player statistics.
  2. Specifies columns to keep (non_numeric_cols and core_stats).
  3. Drops rows with any missing values.
  4. Filters the DataFrame for the given position.
  5. Keeps only the specified columns.
  6. Further filters players who have played more than 5 games.
  7. Applies a per_90fi function to adjust stats per 90 minutes played.
  8. Returns the filtered DataFrame.

Creating Metrics Scores

Another function normalizes the filtered player statistics using MinMax scaling. This process ensures that all metrics are on a similar scale. The function also calculates scores for different performance metrics, which will be used in subsequent analyse

Here’s a breakdown of why the parameters in core_stats are useful for player rating modelling:

Passing:

Playmaking:

Offensive Contribution:

Defensive Contribution:

Ball Carrying & Dribbling:

Overall:

These parameters, when combined, provide a comprehensive picture of a player’s contribution across various aspects of the game. By analyzing these metrics, you can create a rating model that considers a player’s passing ability, playmaking skills, offensive and defensive contributions, and dribbling prowess.

Important Note:

The relative importance of each parameter might vary depending on the specific position (e.g., attackers might be valued more for xG and xA, while defenders might be valued more for Tkl% and Blocks). In future versions of this model I will find a more sophisticated approach to weight these metrics according to positions.

def create_metrics_scores(key_stats_df):
    core_stats = ['90s','Total - Cmp%','KP', 'TB','Sw','PPA', 'PrgP','Tkl%','Blocks', 'Tkl+Int','Clr', 'Carries - PrgDist','SCA90','GCA90','CrsPA','xA', 'Rec','PrgR','xG', 'Sh','SoT']
    passing_metrics = ['Total - Cmp%', 'KP', 'TB', 'Sw', 'PPA', 'PrgP']
    defending_metrics = ['Tkl%', 'Blocks', 'Tkl+Int', 'Clr']
    creation_metrics = ['Carries - PrgDist', 'SCA90', 'GCA90', 'CrsPA', 'xA', 'Rec', 'PrgR']
    shooting_metrics = ['xG', 'Sh', 'SoT']

    scaler = MinMaxScaler()

    stats_normalized = key_stats_df.copy()
    stats_normalized[core_stats] = scaler.fit_transform(stats_normalized[core_stats])

    stats_normalized['Passing_Score'] = stats_normalized[passing_metrics].mean(axis=1) * 10
    stats_normalized['Defending_Score'] = stats_normalized[defending_metrics].mean(axis=1) * 10
    stats_normalized['Creation_Score'] = stats_normalized[creation_metrics].mean(axis=1) * 10
    stats_normalized['Shooting_Score'] = stats_normalized[shooting_metrics].mean(axis=1) * 10

    stats_normalized['Passing_Score'] += stats_normalized.index * 0.001
    stats_normalized['Defending_Score'] += stats_normalized.index * 0.001
    stats_normalized['Creation_Score'] += stats_normalized.index * 0.001
    stats_normalized['Shooting_Score'] += stats_normalized.index * 0.001

    stats_normalized[['Passing_Score', 'Defending_Score', 'Creation_Score', 'Shooting_Score']] = stats_normalized[['Passing_Score', 'Defending_Score', 'Creation_Score', 'Shooting_Score']].clip(lower=0, upper=10)
    return stats_normalized

Explanation:

  1. Defines core_stats and metrics for passing, defending, creation, and shooting.
  2. Initializes a MinMaxScaler to normalize the data.
  3. Normalizes the core_stats columns.
  4. Calculates average scores for each metric group and scales them to a 0-10 range.
  5. Adds a small offset to ensure unique scores.
  6. Clips the scores to ensure they stay within the 0-10 range.
  7. Returns the normalized DataFrame with scores.

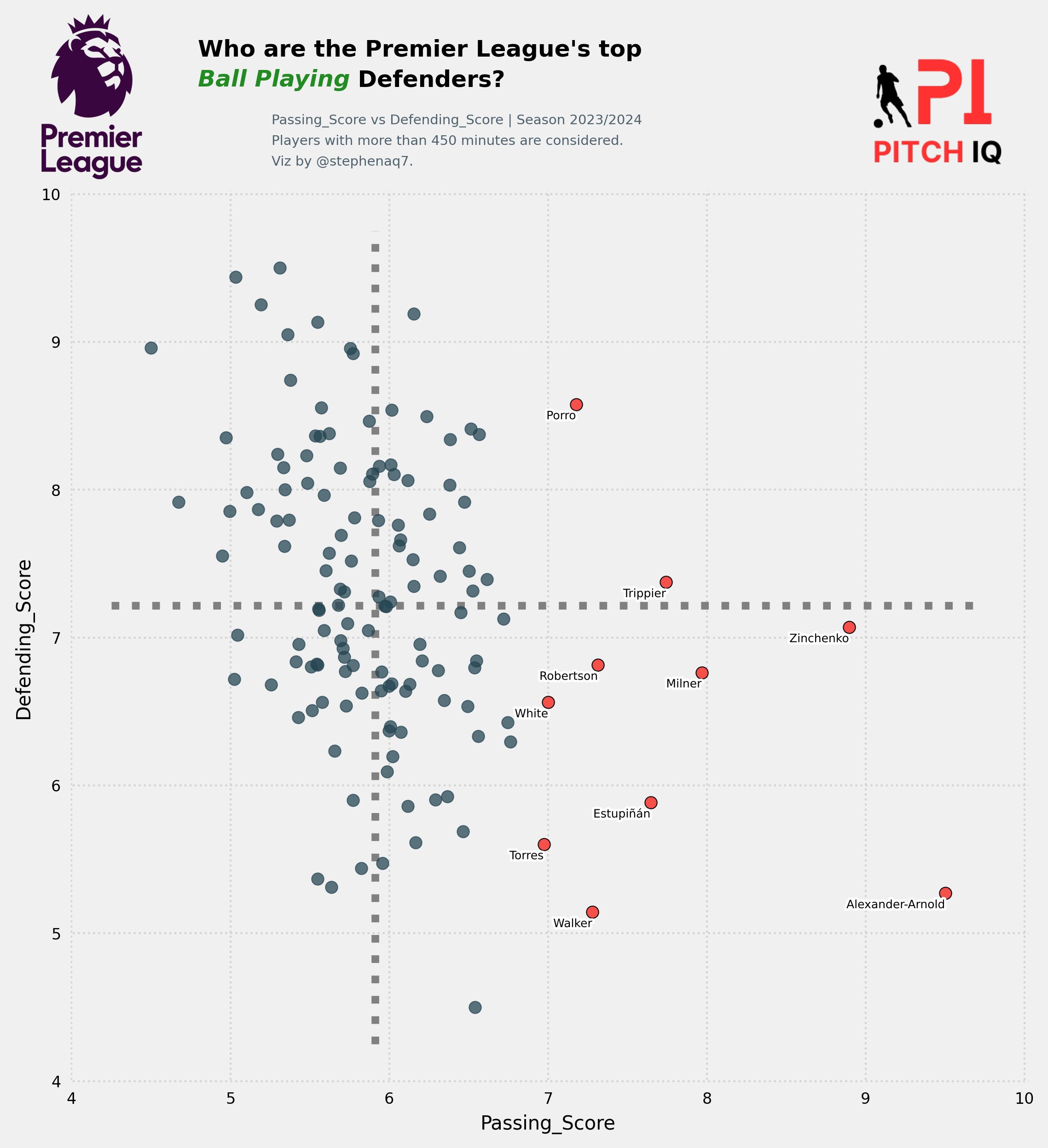
Adjusting Player Rating Range

Setting the minimum and maximum values for the new rating range is important for standardization. This establishes the target range for normalization, ensuring that all ratings fall within the same scale, which is essential for comparison and analysis.

Normalizing the ratings to a common scale allows for consistent comparison across different metrics. The normalization formula adjusts each rating to fall within the specified range, which is important for ensuring that all scores are comparable and can be analyzed together.

def adjust_player_rating_range(dataframe):
    player_ratings = dataframe[['Passing_Score', 'Defending_Score', 'Creation_Score', 'Shooting_Score']]
    
    min_rating = 4.5
    max_rating = 9.5
    
    for col in player_ratings.columns:
        normalized_ratings = min_rating + (max_rating - min_rating) * ((player_ratings[col] - player_ratings[col].min()) / (player_ratings[col].max() - player_ratings[col].min()))
        dataframe[col] = normalized_ratings
    
    return dataframe

pitch_iq_scoring = create_metrics_scores(key_stats_df)
pitch_iq_scoring = adjust_player_rating_range(pitch_iq_scoring)
pitch_iq_scoring = pitch_iq_scoring[['Player','Passing_Score', 'Defending_Score', 'Creation_Score', 'Shooting_Score']]
pitch_iq_scores = pd.merge(key_stats_df, pitch_iq_scoring, on='Player', how='left')

Explanation:

  1. Defines a function to adjust player ratings to a desired range (4.5 to 9.5).
  2. Normalizes scores for each metric column to the specified range.
  3. Merges the adjusted scores back into the main DataFrame based on the player name.

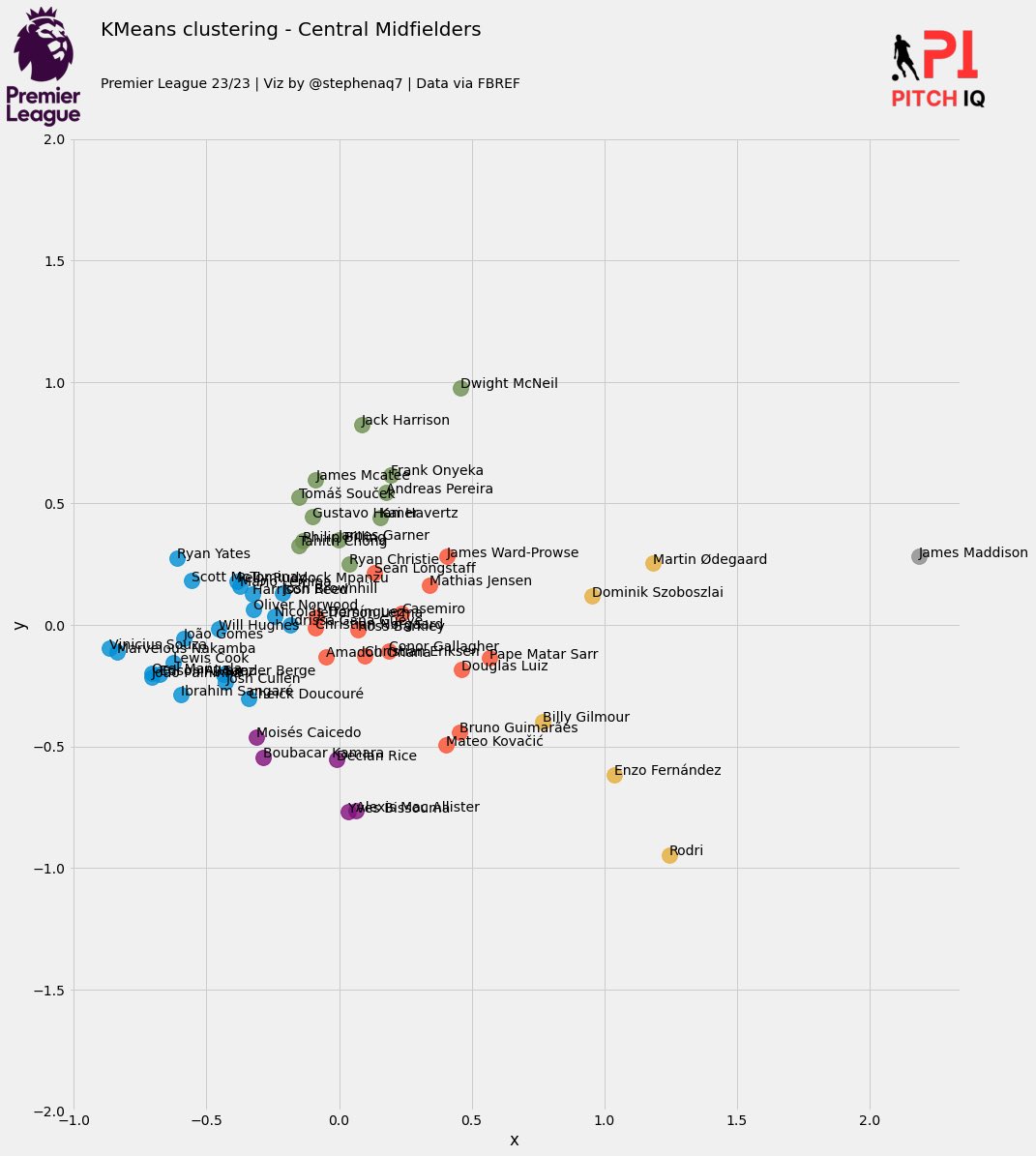
K-Means Clustering for Player Similarity

We perform PCA on the normalized data to reduce its dimensionality while retaining most of the variance. This step helps in simplifying the dataset and identifying the main components that contribute to player performance.

Using the principal components obtained from PCA, we apply K-Means clustering to group players into different clusters based on their performance metrics. This clustering helps in identifying patterns and similarities among players.

def create_kmeans_df(df): 
    KMeans_cols = ['Player','Total - Cmp%','KP', 'TB','Sw','PPA', 'PrgP','Tkl%','Blocks', 'Tkl+Int','Clr', 'Carries - PrgDist','SCA90','GCA90','CrsPA','xA', 'Rec','PrgR','xG', 'Sh','SoT']
    df = df[KMeans_cols]
    player_names = df['Player'].tolist() 
    df = df.drop(['Player'], axis = 1) 
    x = df.values 
    scaler = preprocessing.MinMaxScaler()
    x_scaled = scaler.fit_transform(x)
    X_norm = pd.DataFrame(x_scaled)

    pca = PCA(n_components = 2)
    reduced = pd.DataFrame(pca.fit_transform(X_norm))

    wcss = [] 
    for i in range(1, 11): 
        kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
        kmeans.fit(reduced) 
        wcss.append(kmeans.inertia_)

    kmeans = KMeans(n_clusters=8)
    kmeans = kmeans.fit(reduced)

    labels = kmeans.predict(reduced)
    clusters = kmeans.labels_.tolist()

    reduced['cluster'] = clusters
    reduced['name'] = player_names
    reduced.columns = ['x', 'y', 'cluster', 'name']
    reduced.head()

    return reduced

kmeans_df = create_kmeans_df(key_stats_df)

Explanation:

  1. Filters the DataFrame for the required columns.
  2. Extracts player names and normalizes the feature values.
  3. Reduces the dimensionality of the data using PCA to 2 components.
  4. Computes Within-Cluster Sum of Squares (WCSS) for 1 to 10 clusters.
  5. Applies K-Means clustering with 8 clusters.
  6. Assigns clusters to players and returns a DataFrame with PCA coordinates and cluster assignments.

Finding Similar Players

Certainly! Let’s break down the code find_similar_players and explain the importance of each step:

Function: find_similar_players

def find_similar_players(player_name, df, top_n=15):
    player = df[df['name'] == player_name].iloc[0]
    df['distance'] = np.sqrt((df['x'] - player['x'])**2 + (df['y'] - player['y'])**2)
    
    max_distance = df['distance'].max()  
    
    df['perc_similarity'] = ((max_distance - df['distance']) / max_distance) * 100
    
    similar_players = df.sort_values('distance').head(top_n + 1)  
    similar_players = similar_players[1:] 
    
    return similar_players
Step-by-Step Explanation

Finding the Player of Interest

player = df[df['name'] == player_name].iloc[0]

Identifying the player of interest from the dataframe (df) based on their name (player_name) is crucial. This step ensures that subsequent calculations and comparisons are focused on the correct player, allowing for accurate similarity analysis.

Calculating Euclidean Distance

df['distance'] = np.sqrt((df['x'] - player['x'])**2 + (df['y'] - player['y'])**2)

Computing the Euclidean distance between the player of interest and all other players in the dataset (df) helps quantify their similarity based on spatial coordinates (x and y). This distance metric is fundamental in determining how close or far players are from each other in a multi-dimensional space.

Normalization of Distance

max_distance = df['distance'].max()
df['perc_similarity'] = ((max_distance - df['distance']) / max_distance) * 100

Normalizing the distance to a percentage scale (perc_similarity) standardizes the comparison of similarity across different players. By normalizing, the function ensures that the most similar players have higher percentage scores, making it easier to interpret and compare their similarity based on distance.

  1. Selecting Top Similar Players
similar_players = df.sort_values('distance').head(top_n + 1)
similar_players = similar_players[1:]

Importance: Selecting the top top_n players who are most similar to the player of interest completes the similarity analysis. Sorting the dataframe by distance and excluding the player of interest (who would naturally have a distance of zero) ensures that only truly similar players are included in the final list.

  1. Returning the Result
return similar_players[['name', 'perc_similarity']]

Returning a dataframe containing the names of similar players along with their percentage similarity scores allows for easy interpretation and further analysis. This output can be directly used for recommendations, clustering analysis, or any other application that requires identifying similar entities based on spatial distance.

The find_similar_players function is important because it enables the identification of players who are spatially closest to a given player in terms of their coordinates (x and y). This functionality is crucial in various applications such as player scouting, team formation, or personalized recommendations in sports analytics. It provides a structured approach to understanding player similarity based on spatial data, which can inform strategic decisions in sports management and analysis.

def find_similar_players(player_name, df, top_n=15):
    player = df[df['name'] == player_name].iloc[0]
    df['distance'] = np.sqrt((df['x'] - player['x'])**2 + (df['y'] - player['y'])**2)
    
    max_distance = df['distance'].max()  
    
    df['perc_similarity'] = ((max_distance - df['distance']) / max_distance) * 100
    
    similar_players = df.sort_values('distance').head(top_n + 1)  
    similar_players = similar_players[1:] 
    
    return similar_players

similairty_table = find_similar_players(player_name, kmeans_df)[['name','perc_similarity']]

Explanation:

  1. Finds the player specified by player_name and calculates the Euclidean distance to all other players based on PCA coordinates.
  2. Converts distances to a percentage similarity score.
  3. Sorts players by distance and returns the top N most similar players.

Extracting Key Parameters

params = ['Total - Cmp%','KP', 'PPA', 'PrgP', 'Tkl%', 'Blocks', 'Tkl+Int', 'Clr', 'Carries - PrgDist', 'SCA90', 'xA', 'xG']

Explanation:

  1. Defines a list of key parameters for player comparison.

Preparing Player Data for Comparison

main_player = pitch_iq_scores[pitch_iq_scores['Player'] == player_name][params].values.tolist()
comp_player_1 = mertrics_similarity

[mertrics_similarity['name'] == similar_player_1][params].values.tolist()
comp_player_2 = mertrics_similarity[mertrics_similarity['name'] == similar_player_2][params].values.tolist()

Explanation:

  1. Extracts the key parameter values for the main player and two similar players for comparison.

This code is a comprehensive approach to analyzing player performance by preprocessing data, creating scores, normalizing, clustering, and finding similar players. It uses techniques such as Min-Max scaling, PCA, and K-Means clustering.

Normalizing Parameters for Radar Chart

def normalize_list(values_list):
    normalized = []
    for values in values_list:
        min_val = min(values)
        max_val = max(values)
        normalized_values = [(value - min_val) / (max_val - min_val) for value in values]
        normalized.append(normalized_values)
    return normalized

main_player_norm, comp_player_1_norm, comp_player_2_norm = normalize_list([main_player, comp_player_1, comp_player_2])

Explanation:

  1. Defines a function to normalize each list of parameter values to a 0-1 range.
  2. Normalizes the parameter values for the main player and the two comparison players.

Setting Up for Radar Chart Visualization

import matplotlib.pyplot as plt
import numpy as np

params = ['Total - Cmp%', 'KP', 'PPA', 'PrgP', 'Tkl%', 'Blocks', 'Tkl+Int', 'Clr', 'Carries - PrgDist', 'SCA90', 'xA', 'xG']
num_vars = len(params)

angles = np.linspace(0, 2 * np.pi, num_vars, endpoint=False).tolist()
angles += angles[:1]

def plot_radar_chart(names, values, title):
    fig, ax = plt.subplots(figsize=(8, 8), subplot_kw=dict(polar=True))
    ax.set_theta_offset(np.pi / 2)
    ax.set_theta_direction(-1)
    plt.xticks(angles[:-1], params, color='grey', size=8)
    ax.set_rscale('log')

    for name, value in zip(names, values):
        values = value + value[:1]
        ax.plot(angles, values, linewidth=2, linestyle='solid', label=name)
        ax.fill(angles, values, alpha=0.25)

    plt.legend(loc='upper right', bbox_to_anchor=(0.1, 0.1))
    plt.title(title, size=20, color='grey', y=1.1)
    plt.show()

names = [player_name, similar_player_1, similar_player_2]
values = [main_player_norm[0], comp_player_1_norm[0], comp_player_2_norm[0]]

plot_radar_chart(names, values, 'Player Comparison')

Complete Code Integration

The code integrates various steps to preprocess data, create metric scores, normalize values, cluster players, find similar players, normalize key parameters, and visualize the results in a radar chart. Here is how the complete code looks when put together:

  1. Imports: Imports necessary libraries such as pandas, numpy, matplotlib, and sklearn for data processing, visualization, and machine learning.

  2. Key Statistics Preprocessing:
    • Filters and preprocesses the key statistics for players based on position and removes rows with any NaN values.
    • Converts the statistics to per 90-minute values.
  3. Metrics Scores Creation:
    • Normalizes the core statistics and computes scores for passing, defending, creation, and shooting metrics.
  4. Adjust Player Rating Range:
    • Adjusts the rating range for player scores to a specified range.
  5. K-Means Clustering:
    • Normalizes data, reduces dimensionality using PCA, and applies K-Means clustering to group similar players.
    • Assigns cluster labels to players.
  6. Finding Similar Players:
    • Computes the distance of each player from the target player in the reduced feature space.
    • Determines the similarity percentage and identifies the top similar players.
  7. Normalizing Parameters:
    • Normalizes the parameter values for the radar chart.
  8. Radar Chart Visualization:
    • Sets up the parameters and angles for the radar chart.
    • Defines a function to plot the radar chart, comparing the main player with the two most similar players.

This comprehensive approach enables detailed player performance analysis, similarity comparison, and effective visualization using a radar chart.

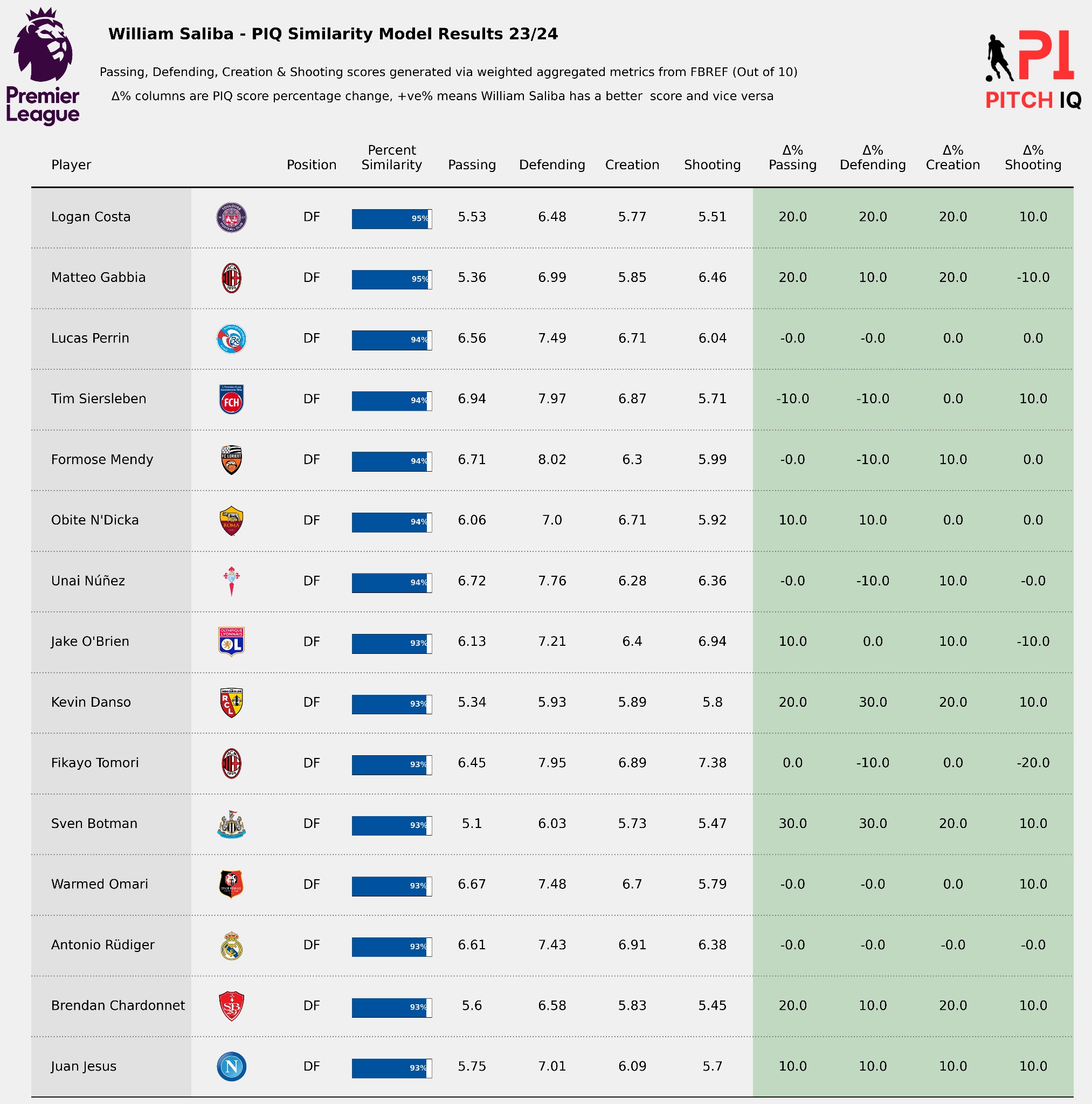
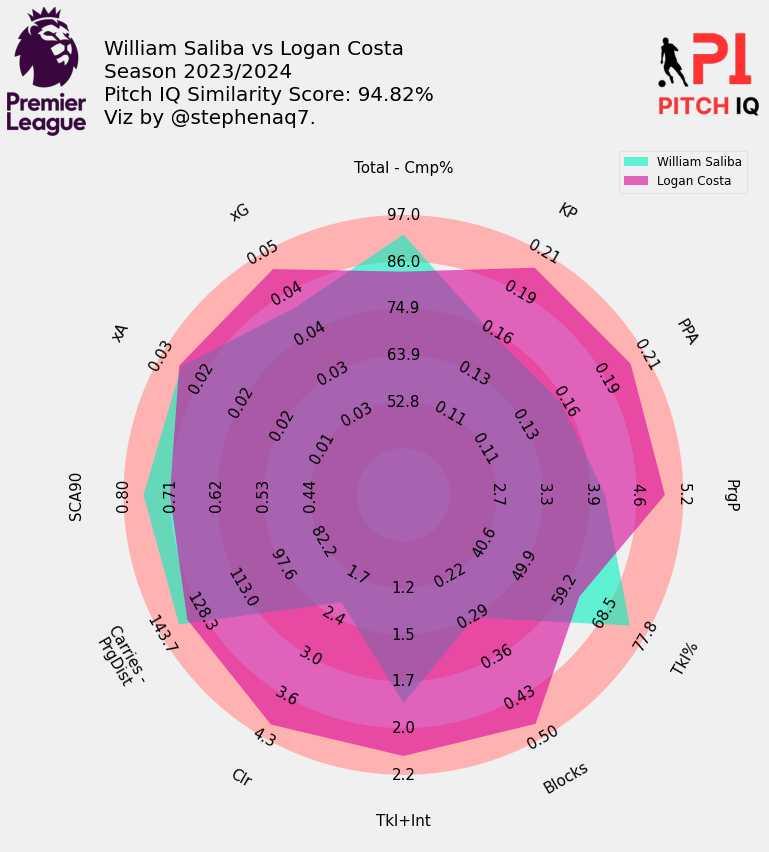
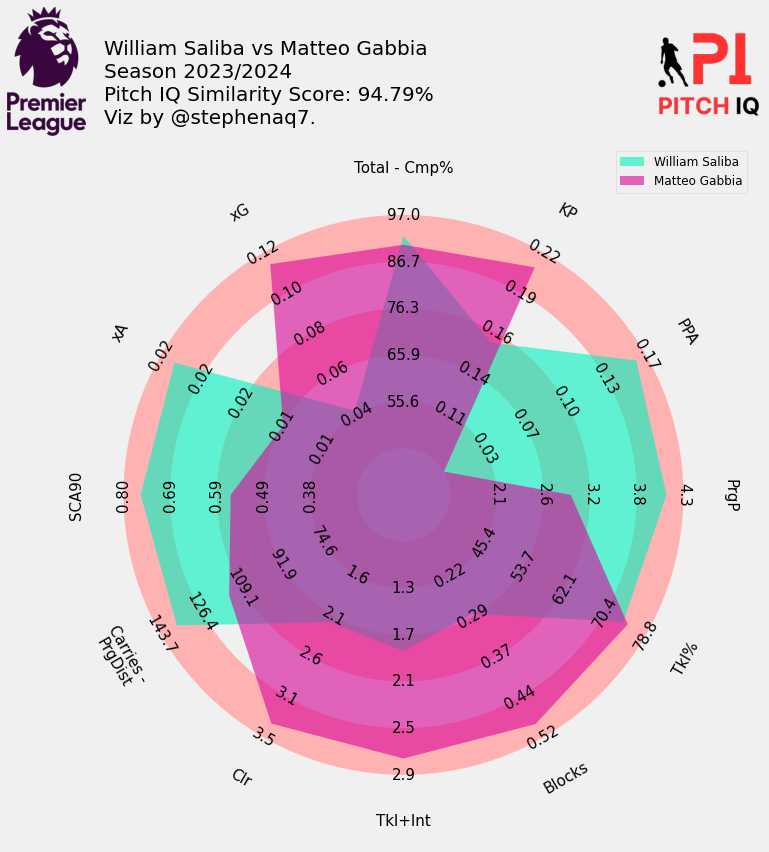
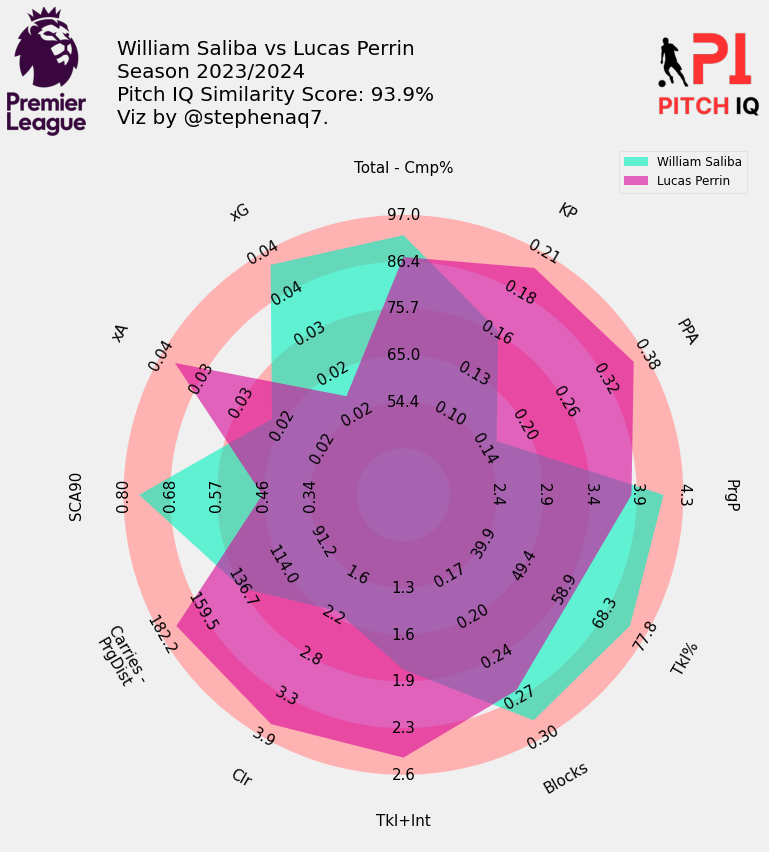
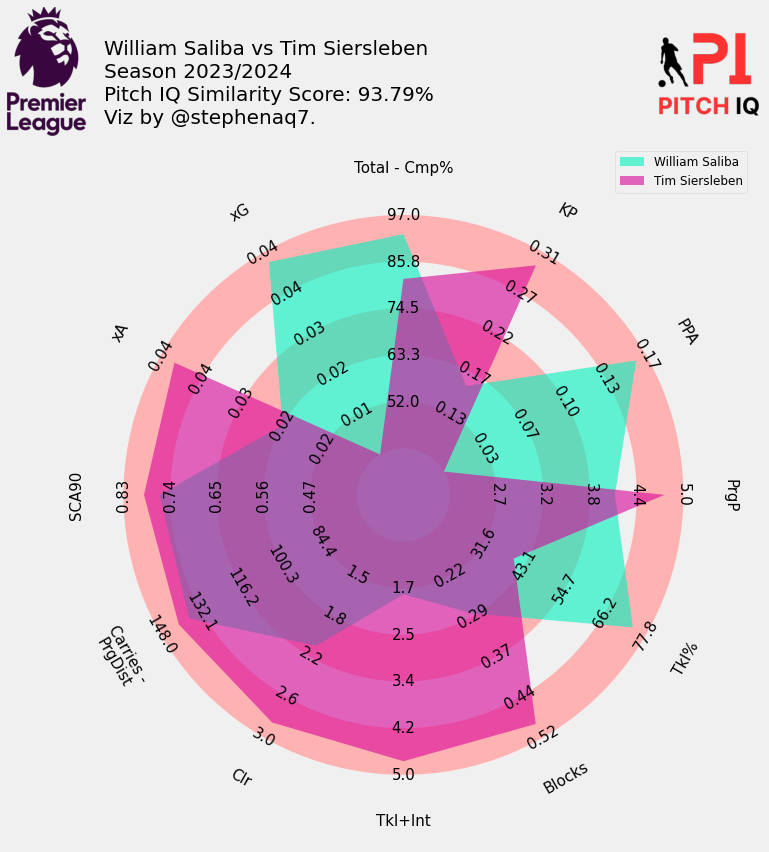
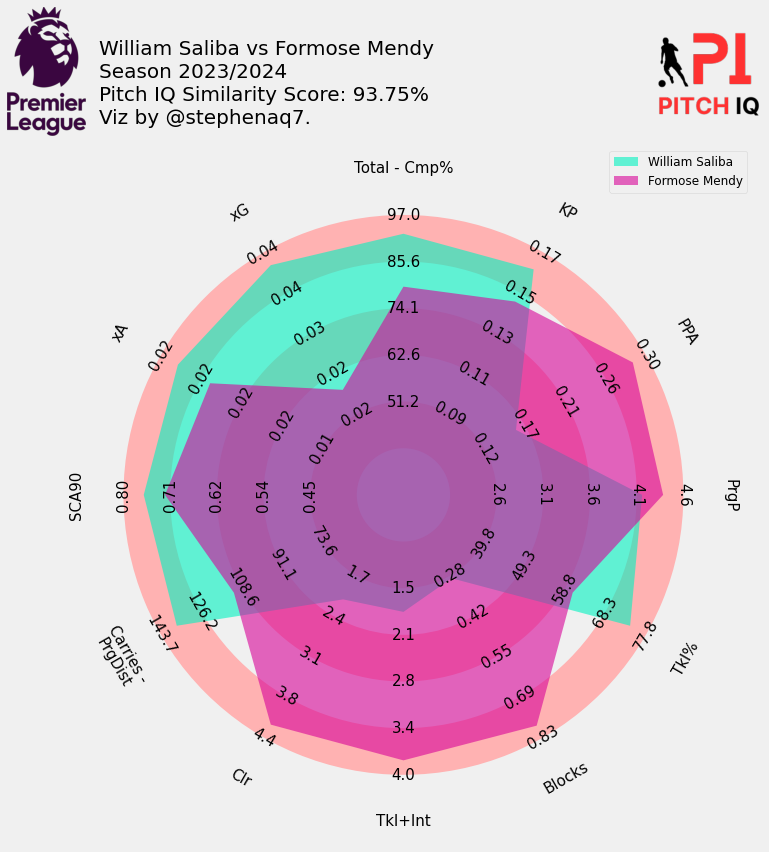
Here are the top 5 players that profile most closely to William Saliba:

l_costa

gabbia

perrin

siersleben

mendy

When Putting it all together, I have created a final visual, showing the top 15 most similar players to Saliba in a handy table.

saliba_sim

Conclusion

In conclusion, this post serves as a valuable addition to a series of tutorials aimed at empowering users to utitlizie data science techniques to better understand manipulate data available from FBREF as well as generating insightful data visualizations,and brief introduction into using python libraries such as sk.learn.

Thanks for reading

Steve